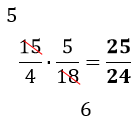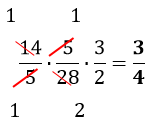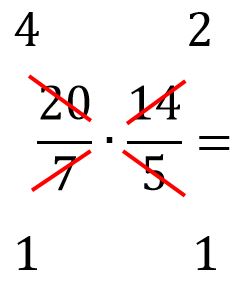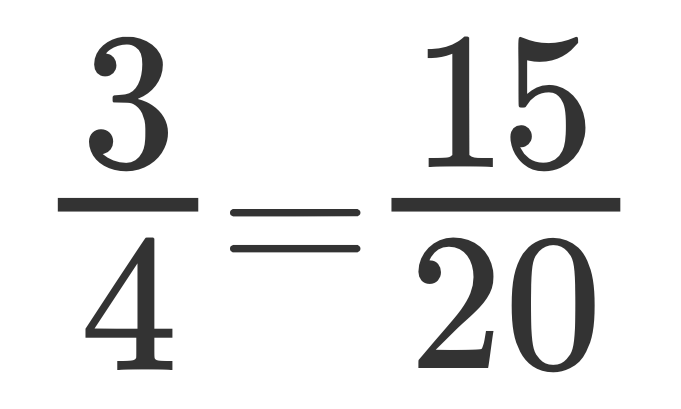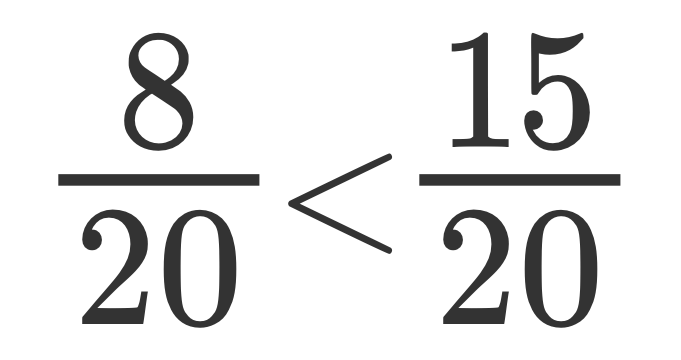In questo articolo vedremo come si calcola la frazione di un numero e viceversa.
Cosa significa determinare la frazione di un numero? Significa determinare un valore che corrisponde ad una parte (frazione) di una certa quantità (numero iniziale).
Solitamente le richieste sono simili a questo esempio: Andrea ha ricevuto un premio al gratta e vinci del valore di €100,00 e decide di spenderne i per un paio di scarpe. Quanto spenderà Andrea?
Per svolgere questo problema si segue un procedimento molto semplice:
- si divide l’intero (cioè i 100 euro) per 4 parti (il denominatore della frazione), ottenendo una parte di 4 (€25,00);
- in seguito, si moltiplica il risultato per 3 parti (il numeratore della frazione) cioè le 3 parti di 4.
Il risultato finale corrisponde alla parte di premio che Andrea decide di utilizzare per l’acquisto delle scarpe.
Ecco il calcolo nel dettaglio:
Altri esempi nella tabella che segue.
| Intero iniziale | Frazione dell’intero | Calcolo e valore finale |
| 150 | ||
| 42 | ||
| 1.245 |
Un altro caso è il seguente: determinare un intero, conoscendo la frazione e il valore corrispondente a questa, quindi passare dalla frazione all’intero.
In altre parole, consideriamo questo esempio: Nel negozio Musicaoggi sono esposte 6 chitarre, che corrispondono ai del totale di quelle a disposizione del proprietario. Quante sono le chitarre in totale?
In questo problema 6 chitarre è una parte del totale (intero), cioè , quindi è necessario un ragionamento inverso rispetto a quello visto all’inizio dell’articolo.
Per svolgere questo problema si segue un procedimento molto semplice:
- si divide la parte (cioè le 6 chitarre) per 3 parti (il numeratore della frazione), ottenendo una parte di 8 (2);
- in seguito, si moltiplica il risultato per 8 parti (il denominatore della frazione), determinando così l’intero.
Il risultato finale corrisponde al numero totale delle chitarre a disposizione nel negozio.
Ecco il calcolo nel dettaglio:
Altri esempi nella tabella che segue.
| Parte dell’intero | Frazione corrispondente | Calcolo e valore dell’intero |
| 45 | ||
| 70 | ||
| 2.348 |
Vai alla pagina con gli esercizi su frazioni, rapporti e proporzioni!
Vai alle altre lezioni su frazioni, rapporti e proporzioni!
Sei un insegnante o, semplicemente, ti incuriosisce il mondo della didattica in generale? Ecco un progetto molto interessante, parallelo a matematicaoggi, dedicato alla didattica: didatticaoggi! Riflessioni, esperienze didattiche e molto altro!