Equazione della retta passante per un punto

6 Luglio 2021 / Alessandro

Se stai cercando come determinare l’equazione della retta passante per un punto, sei nel posto giusto!

Innanzitutto si parte dalla formula generica, cioè l’equazione della retta passante per un punto dato (che chiameremo P):

$y-y_p=m(x-x_p)$

in cui:

$m$ rappresenta il coefficiente angolare, che indica l’inclinazione della retta da determinare;
$x_p$ e $y_p$ sono le coordinate del punto P.

Conoscendo le coordinate del punto P e il coefficiente angolare è possibile determinare l’equazione della retta passante per quel punto, semplicemente sostituendo i valori nell’equazione.

Vediamo ora alcuni esempi.

Esempio 1

Determinare l’equazione della retta passante per il punto A = (3, 4) e con coefficiente angolare uguale a 2.

Riportiamo i dati del nostro esercizio:

$A=(3,4)\rightarrow x_A=3$ e $y_A=4$
$m=+2$

Sostituiamo nell’equazione generica $y-y_p=m(x-x_p)$ i valori sopra riportati:

$y-4=+2(x-3)$

Svolgiamo la moltiplicazione nel secondo membro e portiamo a destra il $-4$ cambiandolo di segno:

$y=+2x-6+4$

Ora è sufficiente sommare algebricamente $-6$ e $+4$ :

$y=+2x-2$

Questa appena ottenuta è l’equazione della retta passante per il punto A di coordinate (3, 4) e con coefficiente angolare uguale a 2.

Ma è corretto? Possiamo verificarlo graficamente!

Innanzitutto è necessario disegnare la retta su un piano cartesiano: per farlo sono necessari due punti, quindi scegliamo a piacere due valori di ascissa e determiniamo le ordinate corrispondenti. In questo modo troveremo due punti che ci permetteranno di tracciare la retta sul piano.

Scegliamo come valori delle ascisse $+1$ e $+4$ :

Ascissa scelta (x)	Ordinata corrispondente (y)	Punto sul grafico
$+1$	$y=+2x-2=+2\cdot(+1)-2=+2-2=0$	$B=(+1,0)$
$+4$	$y=+2x-2=+2\cdot(+4)-2=+8-2=+6$	$C=(+4,+6)$

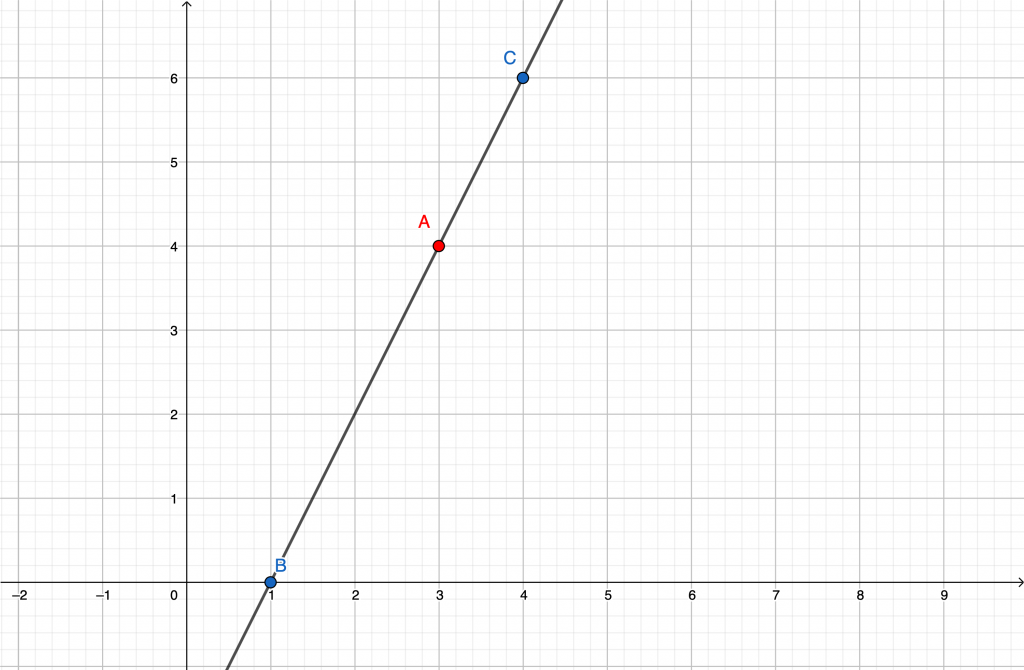
Ora che abbiamo determinato i punti B e C, tracciamo la retta sul piano cartesiano:

Il punto A = (3, 4) appartiene alla retta appena tracciata? Proviamo a posizionarlo sul piano e verifichiamo se è corretto!

Effettivamente il punto A appartiene alla retta tracciata sul piano cartesiano, quindi l’equazione che abbiamo determinato è corretta.

Esempio 2

Determinare l’equazione della retta passante per l’origine e con coefficiente angolare uguale a – 3.

In questo esempio si parla di retta passante per l’origine: in questo caso si fa riferimento all’origine degli assi, cioè il punto O (0, 0). Riportiamo, quindi, i dati del nostro esercizio:

$O=(0,0)\rightarrow x_O=0$ e $y_O=0$
$m=-3$

Sostituiamo nell’equazione generica $y-y_p=m(x-x_p)$ i valori sopra riportati:

$y-0=-3(x-0)$

Svolgiamo la moltiplicazione nel secondo membro:

$y=-3x$

Questa appena ottenuta è l’equazione della retta passante per l’origine degli assi e con coefficiente angolare uguale a – 3.

Anche in questo caso possiamo verificare la correttezza del risultato, disegnando la retta su un piano cartesiano: scegliamo due valori di ascissa a piacere e determiniamo le ordinate corrispondenti. Troveremo due punti che ci permetteranno di tracciare la retta sul piano.

Scegliamo come valori delle ascisse $-1$ e $-2$ :

Ascissa scelta (x)	Ordinata corrispondente (y)	Punto sul grafico
$-1$	$y=-3x=-3\cdot(-1)=+3$	$A=(-1,+3)$
$-2$	$y=-3x=-3\cdot(-2)=+6$	$B=(-2,+6)$

Ora che abbiamo determinato i punti A e B, tracciamo la retta sul piano cartesiano:

Con questo disegno possiamo già verificare che la retta appena tracciata passa per l’origine degli assi, quindi per il punto O (0, 0). Lo fissiamo ugualmente per completezza:

Ora che il grafico è completo, possiamo confermare che l’equazione che abbiamo determinato è corretta.

Se hai ancora dubbi su come si calcola la retta passante per un punto, guarda la videolezione sul canale YouTube matematicaoggi!

Vai alle altre lezioni di geometria!

Sei un insegnante o, semplicemente, ti incuriosisce il mondo della didattica in generale? Ecco un progetto molto interessante, parallelo a matematicaoggi, dedicato alla didattica: didatticaoggi! Riflessioni, esperienze didattiche e molto altro!

Punto medio di un segmento

6 Agosto 2020 / Alessandro

Quando si opera sul piano cartesiano è spesso necessario dover calcolare le coordinate del punto medio di un segmento.

Per determinare le coordinate del punto medio di un segmento sul piano cartesiano è necessario conoscere le coordinate cartesiane dei due estremi del segmento stesso.

Ipotizziamo che i due punti distinti siano A e B e che le loro coordinate cartesiane siano le seguenti:

$A(x_{A}; y_{A})$

$B(x_{B}; y_{B})$

Le coordinate del punto medio del segmento che si ottiene unendo A con B si determinano utilizzando le seguenti formule:

$x_{M}=\frac{x_{A}+x_{B}}{2}$

$y_{M}=\frac{y_{A}+y_{B}}{2}$

Utilizzando queste formule si ottengono, rispettivamente, l’ascissa e l’ordinata del punto medio M.

Vediamo un paio di esempi per applicare le formule sopra indicate.

Esempio 1

Determinare il punto medio del segmento delimitato dai seguenti punti:

$A(4;6)$

$B(14;2)$

Rappresentiamo i punti in un piano cartesiano, unendo A con B:

Ora è sufficiente applicare le formule sopra indicate, sostituendo i valori delle coordinate cartesiane, così come segue:

$x_{M}=\frac{x_{A}+x_{B}}{2}=\frac{4+14}{2}=\frac{18}{2}=9$

$y_{M}=\frac{y_{A}+y_{B}}{2}=\frac{6+2}{2}=\frac{8}{2}=4$

Secondo i calcoli appena eseguiti, il punto medio M ha le seguenti coordinate:

$M(9;4)$

Per verificare la correttezza del risultato possiamo posizionare il punto medio M sul piano cartesiano, così come segue:

Osservando il grafico possiamo confermare che i risultati ottenuti sono corretti: in effetti, la posizione di M equivale al punto medio del segmento delimitato dai punti A e B.

Esempio 2

Determinare il punto medio del segmento delimitato dai seguenti punti:

$A(4;-3)$

$B(-2;-1)$

Rappresentiamo i punti in un piano cartesiano, unendo A con B:

Ora è sufficiente applicare le formule sopra indicate, sostituendo i valori delle coordinate cartesiane, così come segue:

$x_{M}=\frac{x_{A}+x_{B}}{2}=\frac{4-2}{2}=\frac{2}{2}=1$

$y_{M}=\frac{y_{A}+y_{B}}{2}=\frac{-3-1}{2}=\frac{-4}{2}=-2$

Secondo i calcoli appena eseguiti, il punto medio M ha le seguenti coordinate:

$M(1;-2)$

Per verificare la correttezza del risultato possiamo posizionare il punto medio M sul piano cartesiano, così come segue:

Osservando il grafico possiamo confermare che i risultati ottenuti sono corretti: in effetti, la posizione di M equivale al punto medio del segmento delimitato dai punti A e B.

Per chiarire eventuali altri dubbi, ecco una videolezione semplice ed efficace!

Distanza tra due punti

19 Dicembre 20182 Agosto 2019 / Alessandro

Quando si opera sul piano cartesiano è spesso necessario dover calcolare la distanza tra due punti.

Per calcolare la distanza tra due punti sul piano cartesiano è necessario conoscere le coordinate cartesiane di almeno due punti distinti. Unendo questi due punti si forma un segmento.

Si possono distinguere tre casi, a seconda che il segmento che si forma dall’unione dei punti sia orizzontale, verticale, obliquo.

Ipotizziamo che i due punti distinti siano A e B e che le loro coordinate cartesiane siano le seguenti:

$A(x_{A}; y_{A})$

$B(x_{B}; y_{B})$

1° caso: segmento orizzontale

Ipotizziamo che i nostri punti A e B abbiano le seguenti coordinate:

$A(1; 1)$

$B(6; 1)$

Rappresentandoli nel piano cartesiano si ottiene un segmento orizzontale, come si può osservare nel piano sotto rappresentato.

In questo caso, per determinare la distanza tra i punti A e B (quindi, la lunghezza del segmento AB), è sufficiente applicare la seguente formula:

$AB=\left \| x_B-x_A \right \|$

Ciò significa che è sufficiente fare la differenza, in modulo, tra le ascisse dei due punti; quindi avremo:

$AB=\left \| 6-1 \right \|=5$

2° caso: segmento verticale

Ipotizziamo che i nostri punti A e B abbiano le seguenti coordinate:

$A(2; 1)$

$B(2; 7)$

Rappresentandoli nel piano cartesiano si ottiene un segmento verticale, come si può osservare nel piano sotto rappresentato.

In questo caso, per determinare la distanza tra i punti A e B (quindi, la lunghezza del segmento AB), è sufficiente applicare la seguente formula:

$AB=\left \| y_B-y_A \right \|$

Ciò significa che è sufficiente fare la differenza, in modulo, tra le ordinate dei due punti; quindi avremo:

$AB=\left \| 7-1 \right \|=6$

3° caso: segmento obliquo

Ipotizziamo che i nostri punti A e B abbiano le seguenti coordinate:

$A(2; 2)$

$B(6; 5)$

Rappresentandoli nel piano cartesiano si ottiene un segmento obliquo, come si può osservare nel piano sotto rappresentato.

In questo caso, per determinare la distanza tra i punti A e B (quindi, la lunghezza del segmento AB), è sufficiente applicare la seguente formula:

$AB=\sqrt{ (x_B-x_A)^{2}+ (y_B-y_A)^{2}}$

Questa formula non è altro che l’applicazione del Teorema di Pitagora; quindi avremo:

$AB=\sqrt{ (x_B-x_A)^{2}+ (y_B-y_A)^{2}}=\sqrt{ (6-2)^{2}+ (5-2)^{2}}=\sqrt{ 4^{2}+ 3^{2}}=\sqrt{16+9}=\sqrt{25}=5$

Vai alla pagina degli esercizi sulla distanza tra due punti sul piano cartesiano!

Esercizi di geometria

Una pagina dedicata interamente ad esercizi di geometria, divisi per argomenti e di diversi livelli di difficoltà, tutto con un click!

Piano cartesiano

In questa pagina trovi una raccolta di esercizi sul piano cartesiano.

Vai alle lezioni di geometria!