Cosa si intende per angolo somma? E per angolo differenza?
Quando si devono svolgere dei problemi con gli angoli, quelli in cui viene chiesto di determinare l’angolo somma e l’angolo differenza probabilmente sono i più semplici, ma non per questo vanno sottovalutati.
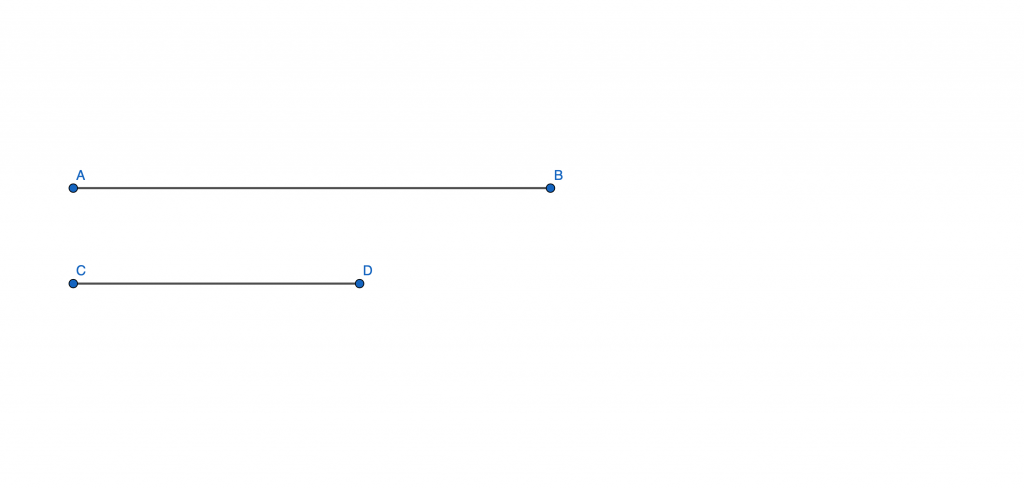
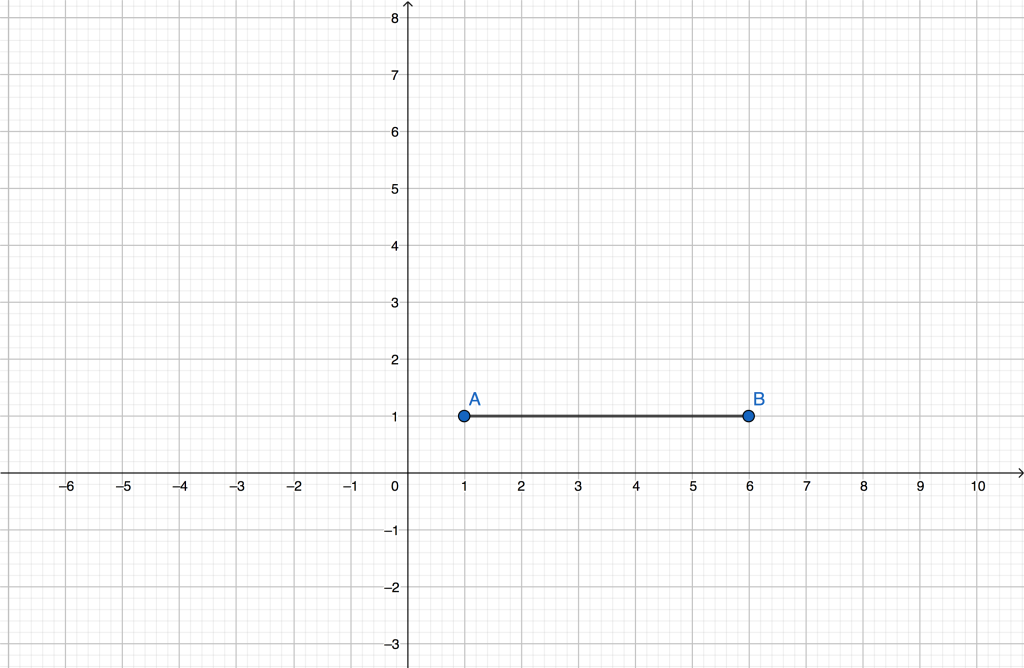
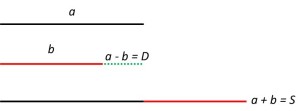
Partiamo definendo due angoli iniziali, α e β:
Angolo somma
Per determinare l’angolo somma degli angoli α e β è possibile utilizzare:
- il metodo grafico, che prevede di disegnare gli angoli α e β in modo consecutivo, facendo corrispondere il secondo lato del primo angolo con il primo lato del secondo angolo, misurando poi l’ampiezza dell’angolo finale;
- il metodo analitico, che prevede – semplicemente – di sommare il valore delle ampiezze dei due angoli α e β.
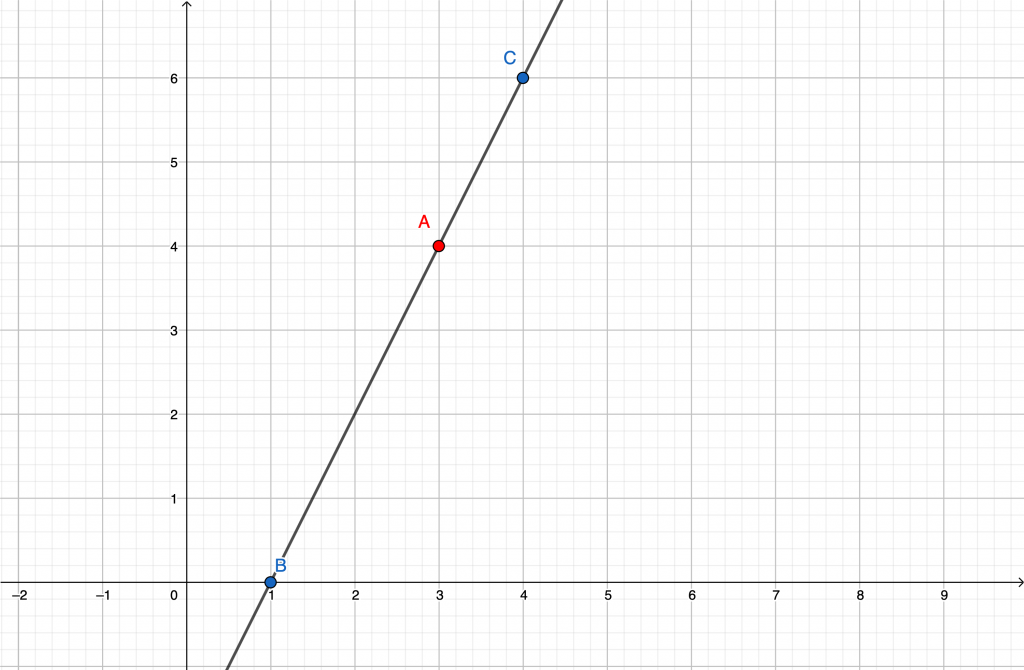
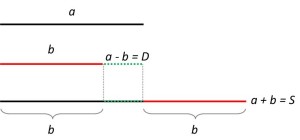
Applichiamo il metodo grafico, rappresentando l’angolo che si crea unendo i due angoli iniziali α e β (consecutivi):
L’angolo somma di α e β è ora quello rappresentato in figura (possiamo chiamarlo δ).
Per quanto riguarda il metodo analitico, supponiamo che gli angoli α e β abbiano le seguenti ampiezze:
- α = 60°
- β = 40°
L’angolo somma si ottiene sommando i valori:
α + β = 60° + 40° = 100°
Angolo differenza
Per determinare l’angolo differenza degli angoli α e β è possibile utilizzare:
- il metodo grafico, che prevede di disegnare l’angolo minore all’interno del maggiore, facendo corrispondere il primo lato di ognuno, misurando poi l’ampiezza dell’angolo che si crea tra i secondi lati dei due angoli;
- il metodo analitico, che prevede – semplicemente – di sottrarre il valore delle ampiezze dei due angoli α e β.
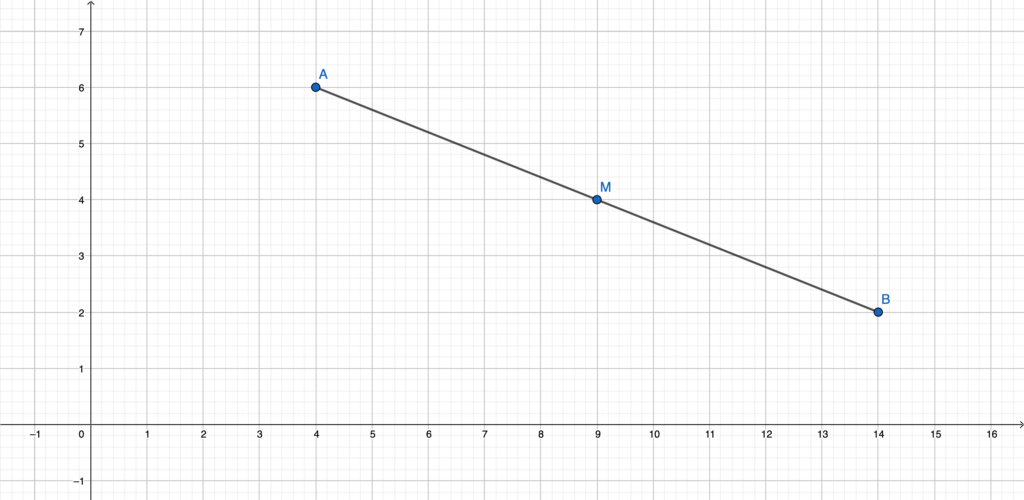
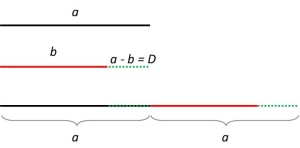
Rappresentiamo con un disegno l’angolo differenza di α e β, utilizzando il metodo grafico (disegniamo l’angolo minore all’interno del maggiore, facendo corrispondere il lato superiore):
L’angolo differenza di α e β è indicato come angolo γ.
Ricordando le ampiezze di α e β, rispettivamente 60° e 40°, l’angolo differenza si ottiene, analiticamente, sottraendo i valori:
α – β = 60° – 40° = 20°
Vai alla pagina sugli esercizi su angolo somma e angolo differenza!
Vai alle altre lezioni di geometria!
Sei un insegnante o, semplicemente, ti incuriosisce il mondo della didattica in generale? Ecco un progetto molto interessante, parallelo a matematicaoggi, dedicato alla didattica: didatticaoggi! Riflessioni, esperienze didattiche e molto altro!