Distanza tra due punti - matematicaoggi

Quando si opera sul piano cartesiano è spesso necessario dover calcolare la distanza tra due punti.

Per calcolare la distanza tra due punti sul piano cartesiano è necessario conoscere le coordinate cartesiane di almeno due punti distinti. Unendo questi due punti si forma un segmento.

Si possono distinguere tre casi, a seconda che il segmento che si forma dall’unione dei punti sia orizzontale, verticale, obliquo.

Ipotizziamo che i due punti distinti siano A e B e che le loro coordinate cartesiane siano le seguenti:

$A(x_{A}; y_{A})$

$B(x_{B}; y_{B})$

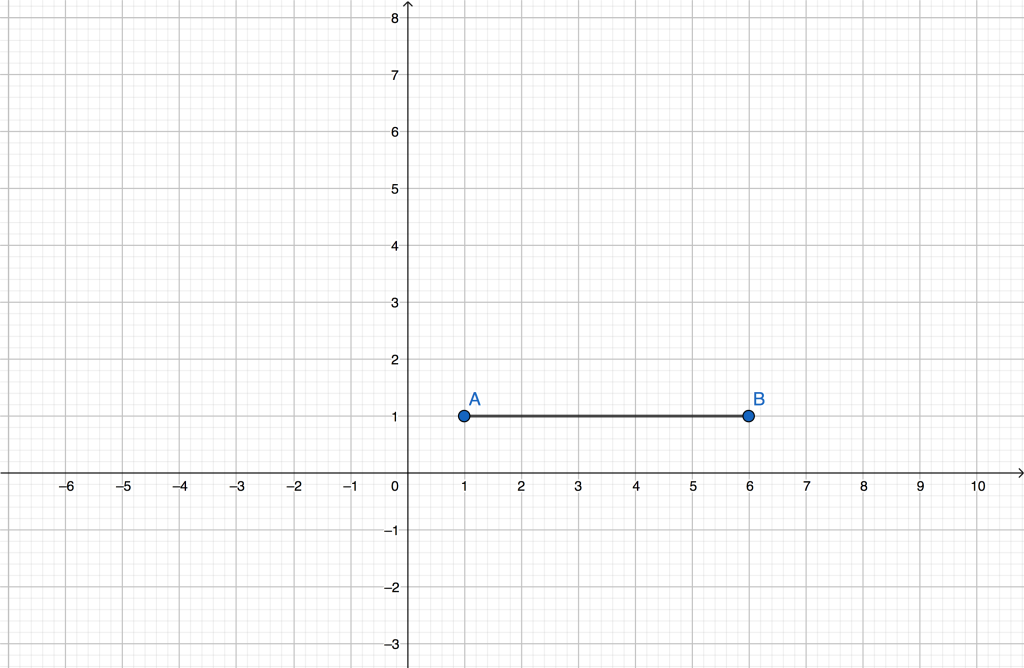
1° caso: segmento orizzontale

Ipotizziamo che i nostri punti A e B abbiano le seguenti coordinate:

$A(1; 1)$

$B(6; 1)$

Rappresentandoli nel piano cartesiano si ottiene un segmento orizzontale, come si può osservare nel piano sotto rappresentato.

In questo caso, per determinare la distanza tra i punti A e B (quindi, la lunghezza del segmento AB), è sufficiente applicare la seguente formula:

$AB=\left \| x_B-x_A \right \|$

Ciò significa che è sufficiente fare la differenza, in modulo, tra le ascisse dei due punti; quindi avremo:

$AB=\left \| 6-1 \right \|=5$

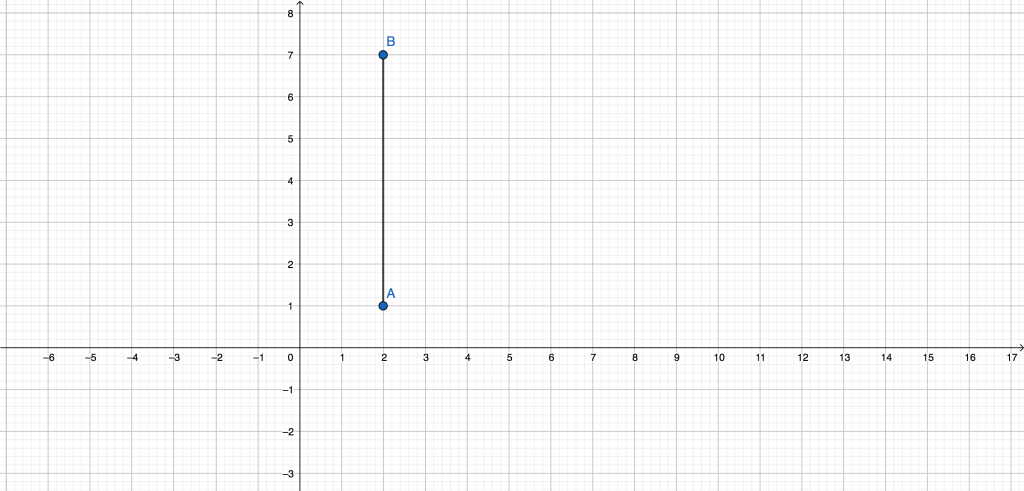
2° caso: segmento verticale

Ipotizziamo che i nostri punti A e B abbiano le seguenti coordinate:

$A(2; 1)$

$B(2; 7)$

Rappresentandoli nel piano cartesiano si ottiene un segmento verticale, come si può osservare nel piano sotto rappresentato.

In questo caso, per determinare la distanza tra i punti A e B (quindi, la lunghezza del segmento AB), è sufficiente applicare la seguente formula:

$AB=\left \| y_B-y_A \right \|$

Ciò significa che è sufficiente fare la differenza, in modulo, tra le ordinate dei due punti; quindi avremo:

$AB=\left \| 7-1 \right \|=6$

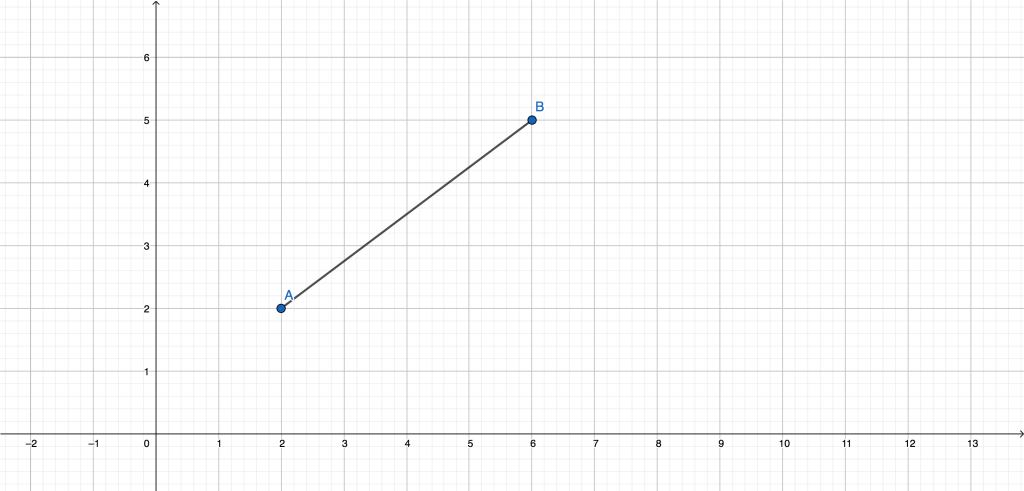
3° caso: segmento obliquo

Ipotizziamo che i nostri punti A e B abbiano le seguenti coordinate:

$A(2; 2)$

$B(6; 5)$

Rappresentandoli nel piano cartesiano si ottiene un segmento obliquo, come si può osservare nel piano sotto rappresentato.

In questo caso, per determinare la distanza tra i punti A e B (quindi, la lunghezza del segmento AB), è sufficiente applicare la seguente formula:

$AB=\sqrt{ (x_B-x_A)^{2}+ (y_B-y_A)^{2}}$

Questa formula non è altro che l’applicazione del Teorema di Pitagora; quindi avremo:

$AB=\sqrt{ (x_B-x_A)^{2}+ (y_B-y_A)^{2}}=\sqrt{ (6-2)^{2}+ (5-2)^{2}}=\sqrt{ 4^{2}+ 3^{2}}=\sqrt{16+9}=\sqrt{25}=5$

Vai alla pagina degli esercizi sulla distanza tra due punti sul piano cartesiano!

Seguici e condividi!