Punto medio di un segmento

Quando si opera sul piano cartesiano è spesso necessario dover calcolare le coordinate del punto medio di un segmento.

Per determinare le coordinate del punto medio di un segmento sul piano cartesiano è necessario conoscere le coordinate cartesiane dei due estremi del segmento stesso.

Ipotizziamo che i due punti distinti siano A e B e che le loro coordinate cartesiane siano le seguenti:

$A(x_{A}; y_{A})$

$B(x_{B}; y_{B})$

Le coordinate del punto medio del segmento che si ottiene unendo A con B si determinano utilizzando le seguenti formule:

$x_{M}=\frac{x_{A}+x_{B}}{2}$

$y_{M}=\frac{y_{A}+y_{B}}{2}$

Utilizzando queste formule si ottengono, rispettivamente, l’ascissa e l’ordinata del punto medio M.

Vediamo un paio di esempi per applicare le formule sopra indicate.

Esempio 1

Determinare il punto medio del segmento delimitato dai seguenti punti:

$A(4;6)$

$B(14;2)$

Rappresentiamo i punti in un piano cartesiano, unendo A con B:

Ora è sufficiente applicare le formule sopra indicate, sostituendo i valori delle coordinate cartesiane, così come segue:

$x_{M}=\frac{x_{A}+x_{B}}{2}=\frac{4+14}{2}=\frac{18}{2}=9$

$y_{M}=\frac{y_{A}+y_{B}}{2}=\frac{6+2}{2}=\frac{8}{2}=4$

Secondo i calcoli appena eseguiti, il punto medio M ha le seguenti coordinate:

$M(9;4)$

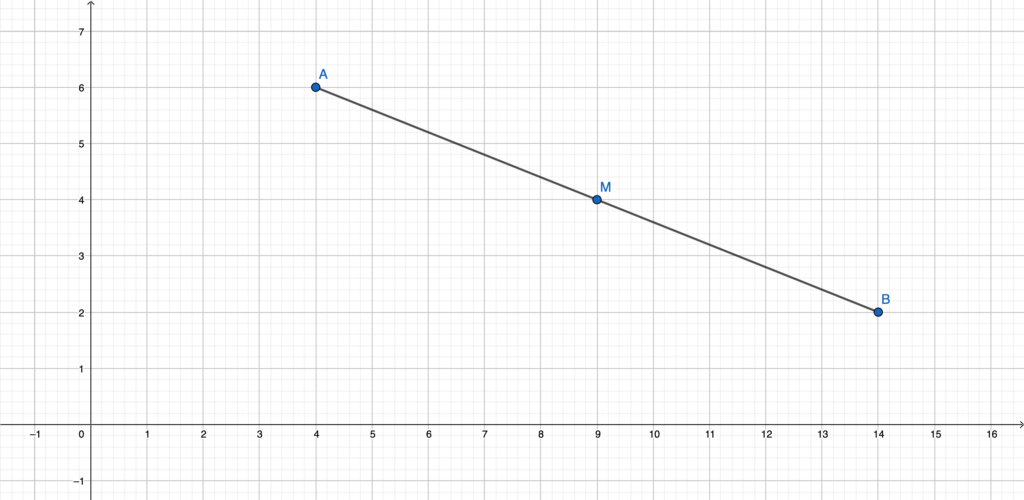
Per verificare la correttezza del risultato possiamo posizionare il punto medio M sul piano cartesiano, così come segue:

Osservando il grafico possiamo confermare che i risultati ottenuti sono corretti: in effetti, la posizione di M equivale al punto medio del segmento delimitato dai punti A e B.

Esempio 2

Determinare il punto medio del segmento delimitato dai seguenti punti:

$A(4;-3)$

$B(-2;-1)$

Rappresentiamo i punti in un piano cartesiano, unendo A con B:

Ora è sufficiente applicare le formule sopra indicate, sostituendo i valori delle coordinate cartesiane, così come segue:

$x_{M}=\frac{x_{A}+x_{B}}{2}=\frac{4-2}{2}=\frac{2}{2}=1$

$y_{M}=\frac{y_{A}+y_{B}}{2}=\frac{-3-1}{2}=\frac{-4}{2}=-2$

Secondo i calcoli appena eseguiti, il punto medio M ha le seguenti coordinate:

$M(1;-2)$

Per verificare la correttezza del risultato possiamo posizionare il punto medio M sul piano cartesiano, così come segue:

Osservando il grafico possiamo confermare che i risultati ottenuti sono corretti: in effetti, la posizione di M equivale al punto medio del segmento delimitato dai punti A e B.

Per chiarire eventuali altri dubbi, ecco una videolezione semplice ed efficace!

Sei un insegnante o, semplicemente, ti incuriosisce il mondo della didattica in generale? Ecco un progetto molto interessante, parallelo a matematicaoggi, dedicato alla didattica: didatticaoggi! Riflessioni, esperienze didattiche e molto altro!

Seguici e condividi!