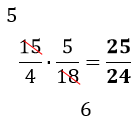Prima di capire come si svolge la divisione di frazioni, è importante chiarire il concetto di reciproco di una frazione.
Se consideriamo la frazione:
il reciproco di questa frazione si ottiene invertendo la posizione di numeratore e denominatore (in pratica si cambiano di posto), quindi si ottiene:
Vediamo alcuni esempi numerici, riportati nella seguente tabella:
| Frazione iniziale | Reciproca |
Chiarito questo concetto, passiamo all’argomento della lezione.
Per eseguire la divisione di frazioni, è necessario – innanzitutto – trasformare la divisione in una moltiplicazione: il dividendo (la prima frazione) rimane uguale, mentre del divisore (la seconda frazione) se ne fa il reciproco (si invertono numeratore e denominatore). In seguito, si risolve la moltiplicazione seguendo le regole della moltiplicazione di frazioni.
Esempio 1:
si trasforma la divisione in moltiplicazione e si scrive la reciproca della seconda frazione, ottenendo:
si procede come per la moltiplicazione, ottenendo:
Esempio 2:
si trasformano le divisioni in moltiplicazioni e si scrivono le reciproche della seconda e della terza frazione, ottenendo:
si procede come per la moltiplicazione, ottenendo:
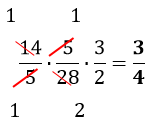Guarda la video lezione nel canale Youtube matematicaoggi!
Vai alla pagina degli esercizi sulla divisione tra frazioni e sulle operazioni con le frazioni in generale!
Questa che abbiamo appena presentato non è l’unica operazione che è possibile svolgere con le frazioni.
Se desideri, puoi accedere ad altre lezioni sulle operazioni con le frazioni! In particolare:
- Addizione di frazioni
- Sottrazione di frazioni
- Moltiplicazione di frazioni
- Potenza di frazioni
- Radice di frazioni
E per finire, non perdere una lezione semplice ma efficace sulle espressioni con le frazioni!
Nel canale Youtube matematicaoggi è presente un’interessante playlist con una serie di videolezioni coinvolgenti, che completano le lezioni sopra elencate.
