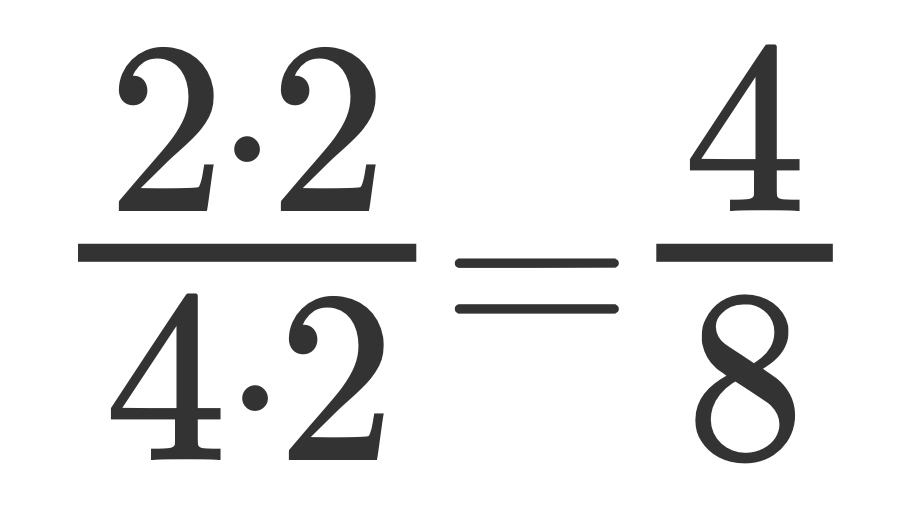Moltiplicando o dividendo (se è possibile) i termini di una frazione per uno stesso numero diverso da 0, si ottiene una frazione equivalente a quella di partenza (proprietà invariantiva o fondamentale delle frazioni).
Data una frazione, le frazioni ad essa equivalenti sono infinite. L’insieme formato da queste frazioni è detto classe di frazioni equivalenti.
In ogni classe di frazioni equivalenti compaiono:
- una e una sola frazione irriducibile (quella i cui termini sono primi tra loro);
- infinite frazioni riducibili (tutte quelle i cui termini ammettono divisori comuni diversi dall’unità).
Esempio:
Consideriamo la frazione
Moltiplichiamo numeratore e denominatore per 2:
Dividiamo numeratore e denominatore per 2:
Le frazioni
sono frazioni equivalenti, cioè rappresentano la stessa parte dell’intero, come si può vedere chiaramente dallo schema sotto riportato.
Guarda la video lezione nel canale Youtube matematicaoggi!
Vai alla pagina degli esercizi sulla proprietà invariantiva delle frazioni!
Scarica il pdf della lezione sulla proprietà invariantiva delle frazioni!
Se questa lezione ti è stata di aiuto, dai un’occhiata alle altre lezioni sulle frazioni:
- Le frazioni;
- Tipi di frazioni;
- Semplificazione di una frazione;
- Riduzione di più frazioni allo stesso denominatore;
- Confronto tra frazioni;
- Operazioni con le frazioni;
- Frazioni con le proprietà delle potenze;
- Espressioni con le frazioni;
- Frazione generatrice di un numero decimale.
Sei un insegnante? Dai un’occhiata a Didatticaoggi: un progetto per chi vive l’avventura dell’insegnamento!